4 项目 1 - 构建 base64 编码器/解码器
作为我们的第一个小项目,我想和你一起实现一个 Base64 编码器/解码器。Base64 是一种将二进制数据转换为文本的编码系统。网络上很大一部分使用 Base64 将二进制数据传输到只能读取文本数据的系统。
现代 base64 最常见的用例基本上是任何电子邮件系统,例如 GMail、Outlook 等。因为电子邮件系统通常使用简单邮件传输协议 (SMTP),这是一种仅支持文本数据的 Web 协议。因此,如果您出于任何原因需要将二进制文件(例如 PDF 或 Excel 文件)作为电子邮件附件发送,这些二进制文件通常会先转换为 base64 编码,然后再包含在 SMTP 消息中。因此,这些电子邮件系统广泛使用 base64 编码来将二进制数据包含在 SMTP 消息中。
4.1 base64算法如何工作?
但是 Base64 编码背后的算法究竟是如何工作的呢?让我们来讨论一下。首先,我将解释一下 Base64 的标度,也就是 64 个字符的标度,它是 Base64 编码系统的基础。
之后,我会解释 base64 编码器背后的算法,它是算法的一部分,负责将消息编码到 base64 编码系统中。之后,我会解释 base64 解码器背后的算法,它是算法的一部分,负责将 base64 消息翻译回其原始含义。
如果您不确定“编码器”和“解码器”之间的区别,请参阅第 4.2 节。
4.1.1 base64 缩放比例
Base64 编码系统基于 0 到 63 的数值范围(因此得名)。该范围中的每个索引都由一个字符表示(即 64 个字符的数值范围)。因此,为了将二进制数据转换为 Base64 编码,我们需要将每个二进制数转换为该“64 个字符的数值范围”中对应的字符。
base64 编码的标度以全部 ASCII 大写字母(A 到 Z)开头,代表该标度的前 25 个索引(0 到 25)。之后,全部 ASCII 小写字母(a 到 z),代表标度中的 26 到 51 的范围。之后,是一位数(0 到 9),代表标度中的 52 到 61 的索引。最后,标度中的最后两个索引(62 和 63)分别用字符+和表示/。
这些是组成 base64 标度的 64 个字符。等号 ( =) 本身不属于标度,但它是 base64 编码系统中的特殊字符。此字符仅用作后缀,用于标记字符序列的结束,或者标记序列中有意义字符的结束。
以下要点总结了 base64 的比例:
- 范围 0 到 25 表示为:ASCII 大写字母
-> [A-Z]; - 范围 26 到 51 表示为:ASCII 小写字母
-> [a-z]; - 范围 52 至 61 表示为:一位数
-> [0-9]; - 索引 62 和 63 分别用字符
+和表示/; - 该字符
=表示序列中有意义字符的结束;
4.1.2创建查找表形式的量表
在代码中表示此比例的最佳方法是将其表示为_查找表_。查找表是计算机科学中加速计算的经典策略。其基本思想是用基本的数组索引操作替换运行时计算(这可能需要很长时间才能完成)。
您无需每次需要时都计算结果,而是一次性计算所有可能的结果,然后将它们存储在一个数组(其行为类似于“表”)中。这样,每次需要使用 Base64 编码的某个字符时,无需耗费大量资源来计算要使用的确切字符,只需从存储了所有 Base64 编码可能字符的数组中检索该字符即可。我们直接从内存中检索所需的字符。
我们可以开始构建一个 Zig 结构体来存储我们的 Base64 解码器/编码器逻辑。我们从Base64下面的结构体开始。目前,该结构体中只有一个数据成员,即成员_table,它代表我们的查找表。我们还有一个init()方法,用于创建对象的新实例Base64,以及一个_char_at()方法,用于“获取索引处的字符”。x”类型的函数。
const Base64 = struct {
_table: *const [64]u8,
pub fn init() Base64 {
const upper = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
const lower = "abcdefghijklmnopqrstuvwxyz";
const numbers_symb = "0123456789+/";
return Base64{
._table = upper ++ lower ++ numbers_symb,
};
}
pub fn _char_at(self: Base64, index: usize) u8 {
return self._table[index];
}
};
换句话说,该_char_at()方法负责获取查找表(即_table结构体数据成员)中与“base64 编码”中特定索引对应的字符。因此,在下面的例子中,我们知道与“base64 编码”中索引 28 对应的字符是字符“c”。
const base64 = Base64.init();
try stdout.print(
"Character at index 28: {c}\n",
.{base64._char_at(28)}
);
Character at index 28: c
4.1.3 base64编码器
Base64 编码器背后的算法通常作用于 3 个字节的窗口。由于每个字节有 8 位,因此 3 个字节构成一组8×3=24位。这对于 base64 算法来说是理想的,因为 24 位可以被 6 整除,从而形成24/6=4每组 6 位。
因此,base64 算法的工作原理是每次将 3 个字节转换为 4 个 base64 字符。它会不断迭代输入字符串,每次 3 个字节,并将其转换为 base64 字符,每次迭代产生 4 个字符。它会不断迭代,不断产生这些“新字符”,直到到达输入字符串的末尾。
现在你可能会想,如果你有一个特定的字符串,其字节数不能被 3 整除,会发生什么?例如,如果你有一个只包含两个字符/字节的字符串,例如“Hi”。在这种情况下,算法会如何表现?你可以在图 4.1中找到答案。你可以在图 4.1中看到,字符串“Hi”在转换为 base64 后变成了字符串“SGk=”:
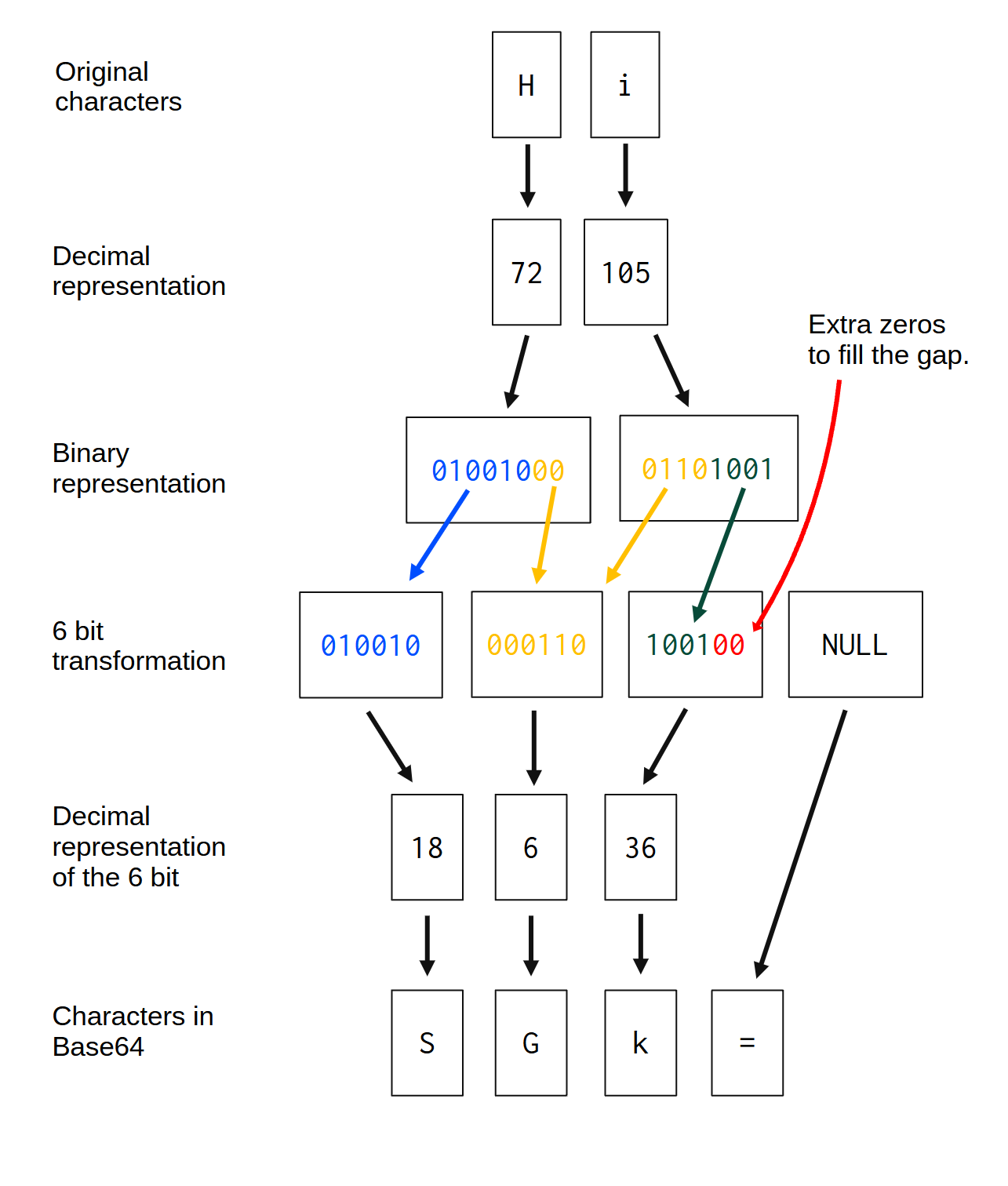
图 4.1:base64 编码器背后的逻辑
以字符串“Hi”为例,它有 2 个字节,也就是 16 位。因此,我们缺少一个完整的字节(8 位)来填充 base64 算法所需的 24 位窗口。该算法首先会检查如何将输入字节分成 6 位一组。
如果算法注意到有一组 6 位不完整,这意味着该组包含nb我吨秒, 在哪里0<nb我吨秒<6,
算法只是在这个组中额外添加一些零来填补所需的空间。这就是为什么在图 4.1中,经过 6 位变换后的第三组中,额外添加了 2 个零来填补空缺。
当一个 6 位组未完全填满时(例如第三个组),会添加额外的零来填补空缺。但是,如果整个 6 位组都为空,或者根本就不存在,该怎么办呢?图 4.1所示的第四个 6 位组就属于这种情况。
第四组是必需的,因为该算法处理 4 组 6 位数据。但输入字符串没有足够的字节来创建第四组 6 位数据。每当整个 6 位数据组为空时,该组就会变成“填充组”。每个“填充组”都会映射到字符=(等号),该字符表示“空”,或者序列中有意义字符的结尾。因此,每当算法生成一个“填充组”时,该组都会自动映射到=。
再举一个例子,如果将字符串“0”作为base64编码器的输入,该字符串将被转换为base64序列“MA==”。字符“0”的二进制表示为序列001100001 。因此,按照图 4.1所示的6位转换,这个字符将产生两个6位组:001100,000000。剩下的两个6位组成为“填充组”。这就是为什么输出序列(MA==)中的最后两个字符是==。
4.1.4 base64解码器
Base64 解码器背后的算法本质上是 Base64 编码器的逆过程。Base64 解码器需要将 Base64 消息转换回其原始含义,即原始的二进制数据序列。
Base64 解码器通常处理 4 个字节的窗口。因为它需要将这 4 个字节转换回原始的 3 个字节序列,而原始的 3 个字节序列又被 Base64 编码器转换成了 4 组 6 位数据。记住,在 Base64 解码器中,我们实际上是在还原 Base64 编码器的转换过程。
输入字符串(base64 编码的字符串)中的每个字节通常会在输出(原始二进制数据)中重新创建两个不同的字节。换句话说,base64 解码器输出的每个字节都是通过将输入中的两个不同字节进行变换或合并而生成的。您可以在图 4.2中直观地看到这种关系:
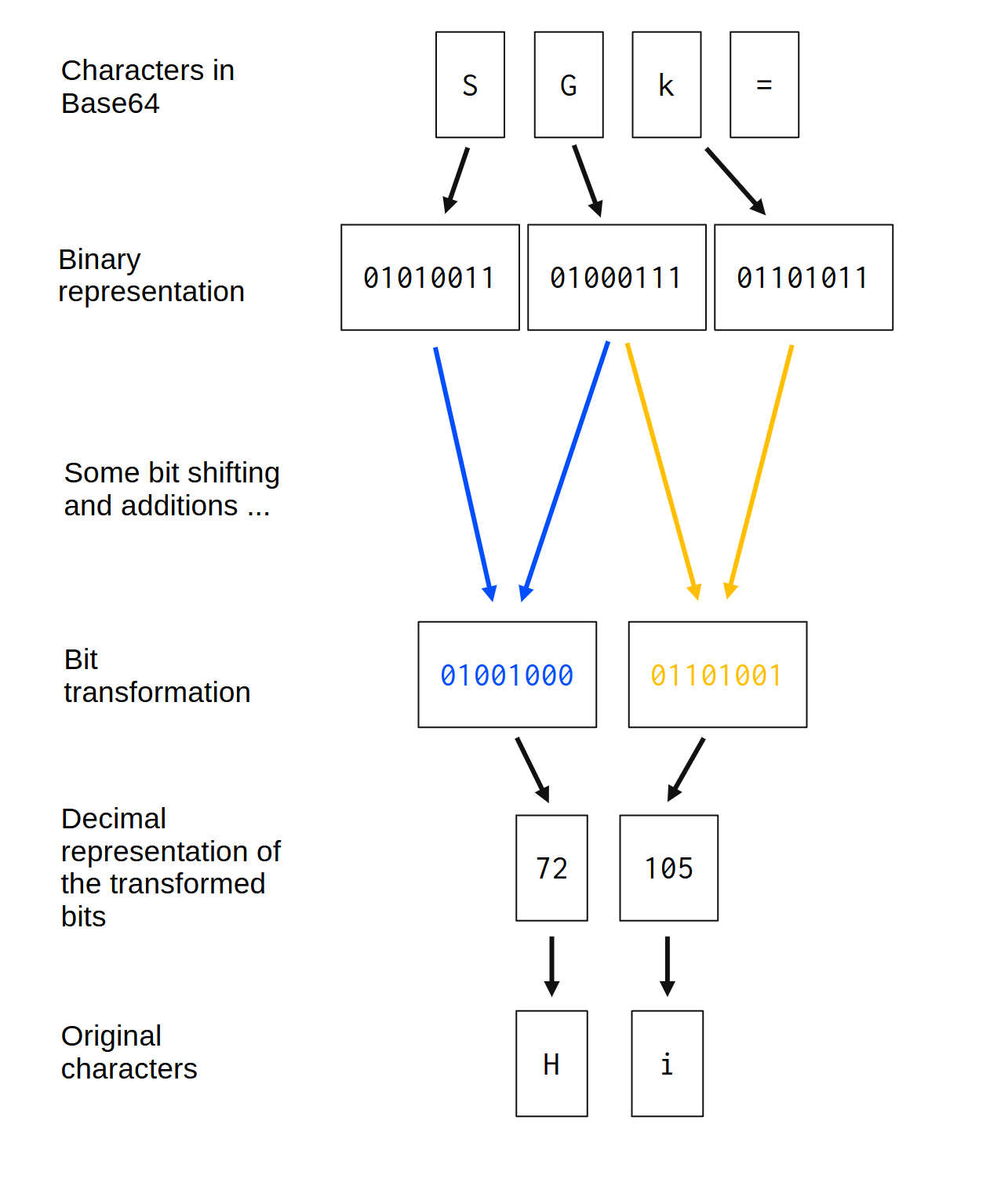
图 4.2:base64 解码器背后的逻辑
确切的转换,或者说,对输入中的每个字节应用到输出字节的具体步骤,在这样的图中很难直观地展现。因此,我在图中将这些转换概括为“一些位移位和加法……”。这些转换将在稍后深入描述。
除此之外,如果你再次查看图 4.2,你会注意到该字符=被算法完全忽略了。记住,这只是一个特殊字符,用于标记 base64 序列中有意义字符的结尾。因此,=base64 编码序列中的每个字符都应该被 base64 解码器忽略。
4.2编码和解码的区别
如果您以前没有使用过 Base64,您可能无法理解“编码”和“解码”之间的区别。本质上,这里的“编码”和“解码”与加密领域中的含义完全相同(即,它们与哈希算法(例如 MD5 算法)中的“编码”和“解码”含义相同)。
因此,“encode” 表示我们要进行编码,或者换句话说,我们要将一些消息转换为 base64 编码系统。我们希望生成一个 base64 字符序列,以在 base64 编码系统中表示原始消息。
相反,“解码”代表逆过程。我们希望解码,或者换句话说,将 Base64 消息转换回其原始内容。因此,在这个过程中,我们输入一个 Base64 字符序列,并输出由该 Base64 字符序列表示的二进制数据。
任何 base64 库通常由以下两部分组成:1)编码器,它是将任何二进制数据序列编码(即转换)为 base64 字符序列的函数;2)解码器,它是将 base64 字符序列转换回原始二进制数据序列的函数。
4.3计算输出的大小
我们需要做的一项任务是计算需要为编码器和解码器的输出预留多少空间。这是一个简单的数学问题,可以在 Zig 中轻松完成,因为每个数组的长度(元素数量)都可以通过查询.len数组的属性轻松访问。
对于编码器来说,其逻辑如下:输入中每出现 3 个字节,输出中就会产生 4 个新字节。因此,我们将输入的字节数除以 3,使用一个上限函数,然后将结果乘以 4。这样,我们就得到了编码器输出的总字节数。
下面的函数_calc_encode_length()封装了这个逻辑。在这个函数中,我们获取输入数组的长度,将其除以 3,然后使用divCeil()Zig 标准库中的函数对结果进行 ceil 运算。最后,我们将最终结果乘以 4 即可得到所需的答案。
另外,你可能已经注意到,如果输入长度小于 3 个字节,那么编码器的输出长度始终为 4 个字节。对于所有小于 3 个字节的输入都是如此,因为正如我在4.1.3 节中所述,该算法在最终结果中始终会生成足够多的“填充组”,以填满 4 个字节的窗口。
const std = @import("std");
fn _calc_encode_length(input: []const u8) !usize {
if (input.len < 3) {
return 4;
}
const n_groups: usize = try std.math.divCeil(
usize, input.len, 3
);
return n_groups * 4;
}
现在,计算解码器输出长度的逻辑稍微复杂一些。但它基本上就是我们在编码器中使用的逻辑的逆:输入中每 4 个字节,解码器就会输出 3 个字节。然而,这次我们需要考虑字符,正如我们在4.1.4 节和图 4.2=中所述,它总是被解码器忽略。
本质上,我们取输入的长度并将其除以 4,然后对结果应用向下取整函数,然后将结果乘以 3,然后从结果中减去=在输入中找到该字符的次数。
下面展示的函数_calc_decode_length()总结了我们之前描述的逻辑。它类似于函数_calc_encode_length()。请注意,除法部分有所不同。还要注意,这次我们使用divFloor()函数对除法的输出进行了向下取整运算(而不是使用 进行向上取整运算divCeil())。
const std = @import("std");
fn _calc_decode_length(input: []const u8) !usize {
if (input.len < 4) {
return 3;
}
const n_groups: usize = try std.math.divFloor(
usize, input.len, 4
);
var multiple_groups: usize = n_groups * 3;
var i: usize = input.len - 1;
while (i > 0) : (i -= 1) {
if (input[i] == '=') {
multiple_groups -= 1;
} else {
break;
}
}
return multiple_groups;
}
4.4构建编码器逻辑
在本节中,我们将开始构建函数背后的逻辑encode(),该函数将负责将消息编码到 base64 编码系统中。如果您急切地想查看这个 base64 编码器/解码器的完整实现源代码,您可以在本书官方仓库的文件夹中找到ZigExamples它。
4.4.1 6位变换
图 4.1中所示的 6 位变换是 base64 编码器算法的核心部分。通过理解代码中如何实现这一变换,算法的其余部分将变得更容易理解。
本质上,这种 6 位转换是借助位运算符完成的。位运算符对于任何类型的位级低级运算都至关重要。对于 Base64 算法,需要使用位左移( <<)、位右移( >>) 和_位与_( &) 运算符。它们是 6 位转换的核心解决方案。
在这个转换过程中,我们需要考虑三种不同的情况。首先,是理想情况,即我们有一个包含 3 个字节的理想窗口可供处理。其次,是只有 2 个字节的窗口可供处理。最后,是只有一个字节的窗口可供处理。
在这三种情况下,6 位转换的工作原理略有不同。为了便于解释,我将使用 变量output引用 base64 编码器输出的字节,使用 变量input引用编码器输入的字节。
因此,如果您有 3 个字节的完美窗口,则以下是 6 位转换的步骤:
output[0]是通过将位从input[0]两个位置向右移动而生成的。output[1]通过将两个分量相加而得出。首先,取其中的最后两位input[0],然后将其向左移动四位。然后,将这input[1]四位向右移动。将这两个分量相加。output[2]通过将两个分量相加而得出。首先,从中取出最后四位input[1],然后将它们向左移动两位。然后,将这input[2]六位向右移动。将这两个分量相加。output[3]是通过从中取出最后六位生成的input[2]。
这是最理想的情况,我们有一个包含 3 个字节的完整窗口可供处理。为了尽可能清晰地说明,图 4.3以直观的方式演示了上述步骤 2 的工作原理。因此,output编码器中的第二个字节是通过从输入中取出第一个字节(深紫色)和第二个字节(橙色)生成的。您可以看到,在处理结束时,我们得到了一个新字节,它包含 中第一个字节的后 2 位input以及 中第二个字节的前 4 位input。
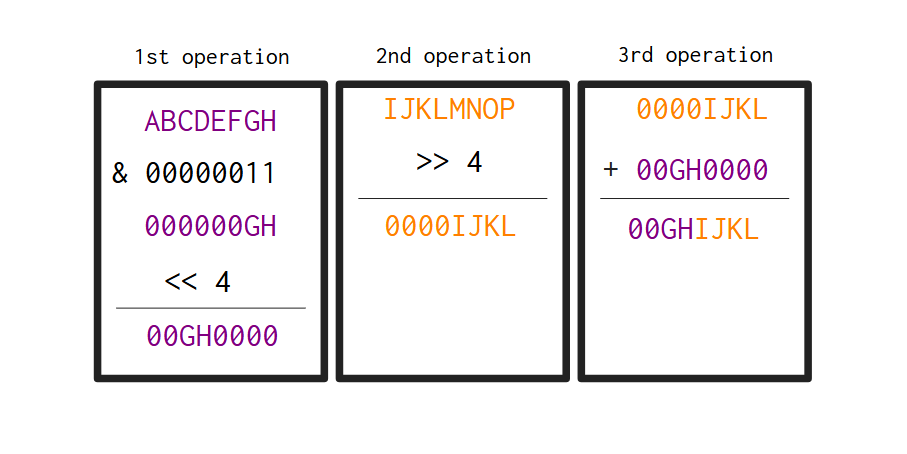
图 4.3:编码器输出中的第 2 个字节是如何由输入的第 1 个字节(深紫色)和第 2 个字节(橙色)产生的。
另一方面,我们必须为没有完美 3 字节窗口的情况做好准备。如果窗口大小为 2 字节,那么步骤 3 和 4(即产生字节output[2]和output[3])会略有变化,最终变成:
output[2]是通过从中取出最后 4 位input[1],然后将它们向左移动两个位置而得到的。output[3]是角色'='。
最后,如果您有一个单字节窗口,则步骤 2 至 4 将产生字节output[1],output[2]并output[3]发生变化,变为:
output[1]是通过从中取出最后两位input[0],然后将它们向左移动四位而得到的。output[2]并且output[3]是 角色=。
如果这些要点让您感到困惑,您可能会发现表 4.1更直观。该表将所有这些逻辑统一到一个简单的表中。请注意,该表还提供了 Zig 中创建相应输出字节的精确表达式。
表 4.1:在不同的窗口设置下,6 位转换如何转换为代码。
| 窗口中的字节数 | 输出中的字节索引 | 在代码中 |
|---|---|---|
| 3 | 0 | 输入[0] >> 2 |
| 3 | 1 | ((输入[0] & 0x03) << 4) + (输入[1] >> 4) |
| 3 | 2 | ((输入[1] & 0x0f) << 2) + (输入[2] >> 6) |
| 3 | 3 | 输入[2] & 0x3f |
| 2 | 0 | 输入[0] >> 2 |
| 2 | 1 | ((输入[0] & 0x03) << 4) + (输入[1] >> 4) |
| 2 | 2 | ((输入[1] & 0x0f) << 2) |
| 2 | 3 | '=' |
| 1 | 0 | 输入[0] >> 2 |
| 1 | 1 | ((输入[0] & 0x03) << 4) |
| 1 | 2 | '=' |
| 1 | 3 | '=' |
4.4.2 Zig 中的位移位
Zig 中的位移位与 C 语言中的位移位类似。C 语言中所有位运算符在 Zig 中均可用。在 base64 编码器算法中,它们对于产生我们想要的结果至关重要。
对于不熟悉这些运算符的人来说,它们是在值的位级别上进行操作的运算符。这意味着这些运算符获取构成值的位,并以某种方式对其进行更改。这最终也会改变值本身,因为该值的二进制表示发生了变化。
我们已经在图 4.3中看到了位移位产生的效果。让我们用 Base64 编码器输出的第一个字节作为另一个例子来说明位移位的含义。这是输出中 4 个字节中最容易构建的字节。因为我们只需要使用_位移位_运算符( >>) 将输入中第一个字节的位向右移动两位即可。
以图 4.1中使用的字符串“Hi”为例,该字符串的第一个字节是“H”,也就是01001000二进制序列。如果我们将该字节的位向右移动两位,就得到了00010010结果序列。这个二进制序列既是十进制值18,也是0x12十六进制值。注意,“H”的前 6 位被移动到了字节的末尾。通过此操作,我们得到了输出的第一个字节。
const std = @import("std");
const stdout = std.io.getStdOut().writer();
pub fn main() !void {
const input = "Hi";
try stdout.print("{d}\n", .{input[0] >> 2});
}
18
如果你回想一下图 4.1,输出中的第一个字节应该相当于 6 位组010010。虽然视觉上有所不同,但序列010010和00010010语义上是相同的。它们的含义相同。它们都用十进制表示数字 18,用十六进制表示值0x12。
所以,不要太在意“6 位组”这个因素。我们不一定需要得到一个 6 位序列作为结果。只要我们得到的 8 位序列的含义与 6 位序列相同,就没问题了。
4.4.3使用&运算符选择特定位
如果你回到4.4.1 节,你会发现,为了生成输出中的第二和第三个字节,我们需要从输入字符串的第一和第二个字节中选择特定的位。但是我们该怎么做呢?答案依赖于_按位与_( &) 运算符。
图4.3已经展示了该运算符对其操作数的 位产生的影响&。让我们对其进行更清晰的描述。
简而言之,该&运算符对其操作数的位执行逻辑与运算。更详细地说,该运算符将&第一个操作数的每个位与第二个操作数的相应位进行比较。如果两个位都为 1,则将相应的结果位设置为 1。否则,将相应的结果位设置为 0 (Microsoft 2021)。
因此,如果我们将此运算符应用于二进制序列1000100,则00001101此运算的结果为二进制序列00000100。因为在两个二进制序列中,只有第六个位置的值是 1。因此,在两个二进制序列中,任何未设置为 1 的位置,在最终的二进制序列中都会得到 0 位。
在这种情况下,我们会丢失两个序列的原始位值信息。因为我们不再知道最终二进制序列中的这个 0 位是 0 与 0 组合而成,还是 1 与 0 组合而成,又或者 0 与 1 组合而成。
举个例子,假设你有一个二进制序列10010111,用十进制表示就是151。那么如何得到一个只包含该序列第三位和第四位的新二进制序列呢?
我们只需使用运算符将此序列与00110000(0x30十六进制的 )组合即可&。注意,此二进制序列中只有第三和第四个位置被设置为 1。因此,两个二进制序列中只有第三和第四个值可能保留在输出中。输出序列中所有剩余位置都被设置为零,即00010000(十进制的 16)。
const std = @import("std");
const stdout = std.io.getStdOut().writer();
pub fn main() !void {
const bits = 0b10010111;
try stdout.print("{d}\n", .{bits & 0b00110000});
}
16
4.4.4为输出分配空间
正如我在3.1.4 节中所述,要将对象存储在堆栈中,该对象需要在编译时具有已知且固定的长度。这对于我们的 Base64 编码器/解码器而言是一个重要的限制。因为输出的大小(来自编码器和解码器)直接取决于输入的大小。
考虑到这一点,我们无法在编译时知道编码器和解码器的输出大小。所以,如果我们无法在编译时知道输出的大小,就意味着我们无法将编码器和解码器的输出都存储在堆栈中。
因此,我们需要将此输出存储在堆上,并且正如我在3.1.5 节中所述,我们只能使用分配器对象将对象存储在堆上。因此,encode()和decode()函数的参数中都需要有一个分配器对象,因为我们确切地知道,在这些函数体中的某个时刻,我们需要在堆上分配空间来存储这些函数的输出。
这就是为什么我在本书中介绍的encode()和函数都有一个名为的参数,它接收一个分配器对象作为输入,该对象由Zig 标准库中的类型标识。decode()``allocator``std.mem.Allocator
4.4.5编写encode()函数
现在我们已经对位运算符的工作原理以及它们如何帮助我们实现想要的结果有了基本的了解。现在,我们可以将图 4.1和表 4.1中描述的所有逻辑封装到一个函数中,并将其添加到我们在4.1.2 节Base64中开始的结构体定义中。
您可以在下面找到该encode()函数。请注意,该函数的第一个参数是Base64结构体本身。因此,这个参数清楚地表明该函数是Base64结构体的一个方法。
由于encode()函数本身相当长,Base64为了简洁起见,我特意省略了源代码中的结构体定义。因此,只需记住此函数是Base64结构体中的公共函数(或公共方法)。
此外,该encode()函数还有另外两个参数:
input是要以 base64 编码的字符输入序列;allocator是在必要的内存分配中使用的分配器对象。
我在第 3.3 节中描述了你需要了解的关于分配器对象的所有知识。所以,如果你不熟悉它们,我强烈建议你回到那一节并仔细阅读。通过查看encode()函数,你会发现我们使用这个分配器对象分配了足够的内存来存储编码过程的输出。
函数中的主 for 循环负责遍历整个输入字符串。在每次迭代中,我们使用一个count变量来计算当前的迭代次数。当迭代count次数达到 3 时,我们尝试对临时缓冲区对象 ( ) 中累积的 3 个字符(或字节)进行编码buf。
对这 3 个字符进行编码并将结果存储在output变量中后,我们将count变量重置为零,并在循环的下一次迭代中重新开始计数。如果循环到达字符串末尾,并且count变量小于 3,则表示临时缓冲区包含输入的最后 1 或 2 个字节。这就是为什么我们if在 for 循环后添加了两个语句,分别处理每种可能的情况。
pub fn encode(self: Base64,
allocator: std.mem.Allocator,
input: []const u8) ![]u8 {
if (input.len == 0) {
return "";
}
const n_out = try _calc_encode_length(input);
var out = try allocator.alloc(u8, n_out);
var buf = [3]u8{ 0, 0, 0 };
var count: u8 = 0;
var iout: u64 = 0;
for (input, 0..) |_, i| {
buf[count] = input[i];
count += 1;
if (count == 3) {
out[iout] = self._char_at(buf[0] >> 2);
out[iout + 1] = self._char_at(
((buf[0] & 0x03) << 4) + (buf[1] >> 4)
);
out[iout + 2] = self._char_at(
((buf[1] & 0x0f) << 2) + (buf[2] >> 6)
);
out[iout + 3] = self._char_at(buf[2] & 0x3f);
iout += 4;
count = 0;
}
}
if (count == 1) {
out[iout] = self._char_at(buf[0] >> 2);
out[iout + 1] = self._char_at(
(buf[0] & 0x03) << 4
);
out[iout + 2] = '=';
out[iout + 3] = '=';
}
if (count == 2) {
out[iout] = self._char_at(buf[0] >> 2);
out[iout + 1] = self._char_at(
((buf[0] & 0x03) << 4) + (buf[1] >> 4)
);
out[iout + 2] = self._char_at(
(buf[1] & 0x0f) << 2
);
out[iout + 3] = '=';
iout += 4;
}
return out;
}
4.5构建解码器逻辑
现在,我们可以专注于编写 Base64 解码器逻辑了。记住,图 4.2中提到,Base64 解码器执行的是编码器的逆过程。因此,我们需要做的就是编写一个函数来执行我在4.4 节decode()中介绍的逆过程。
4.5.1将 base64 字符映射到其索引
为了解码 base64 编码的消息,我们需要做的一件事是计算在解码器输入中遇到的每个 base64 字符在 base64 比例中的索引。
换句话说,解码器接收一个 base64 字符序列作为输入。我们需要将此字符序列转换为一个索引序列。这些索引是每个字符在 base64 编码中的索引。这样,我们就得到了在编码器过程中 6 位转换步骤中计算出的值/字节。
可能有更好/更快的方法来计算这个,尤其是使用“分而治之”类型的策略。但目前,我对简单的“蛮力”策略感到满意。_char_index()下面的函数包含此策略。
我们本质上是在用 base64 编码循环遍历_查找表_,并将得到的字符与 base64 编码中的每个字符进行比较。如果匹配,则返回该字符在 base64 编码中的索引作为结果。
请注意,如果输入字符为'=',函数将返回索引 64,这在标度中“超出范围”。但是,正如我在4.1.1 节中所述,该字符'='本身不属于 base64 标度。它是 base64 中一个特殊且无意义的字符。
还要注意,由于参数的存在,这个_char_index()函数实际上是我们结构体中的一个方法。同样,为了简洁起见,我在这个例子中省略了结构体的定义。Base64``self``Base64
fn _char_index(self: Base64, char: u8) u8 {
if (char == '=')
return 64;
var index: u8 = 0;
for (0..63) |i| {
if (self._char_at(i) == char)
break;
index += 1;
}
return index;
}
4.5.2 6位变换
再次强调,该算法的核心部分是 6 位变换。如果我们理解了执行此变换的必要步骤,那么算法的其余部分就会变得容易得多。
首先,在实际进行 6 位转换之前,我们需要确保使用_char_index()来将 Base64 字符序列转换为索引序列。因此,下面的代码片段对于即将完成的工作至关重要。 的结果_char_index()存储在一个临时缓冲区中,我们将在 6 位转换中使用这个临时缓冲区,而不是实际的对象input。
for (0..input.len) |i| {
buf[i] = self._char_index(input[i]);
}
现在,base64 解码器不再对输入中每个包含 3 个字符的窗口生成 4 个字节(或 4 个字符)的输出,而是对输入中每个包含 4 个字符的窗口生成 3 个字节(或 3 个字符)的输出。这又是一个逆过程。
因此,生成输出中的 3 个字节的步骤如下:
output[0]由两个分量相加得到。首先,将buf[0]两个位置的位向左移动。然后,将buf[1]四个位置的位向右移动。最后,将这两个分量相加。output[1]通过将两个分量相加而得到。首先,将位从buf[1]左移 4 位。然后,将位从buf[2]右移 2 位。最后,将这两个分量相加。output[2]是通过将两个分量相加而得到的。首先,将位从buf[2]六位向左移动。然后将结果与 相加buf[3]。
在继续之前,让我们先想象一下这些变换是如何生成编码过程之前的原始字节的。首先,回想一下4.4 节中介绍的编码器执行的 6 位变换。编码器输出的第一个字节是通过将输入的第一个字节中的位向右移动两位而生成的。
例如,如果编码器输入的第一个字节是序列ABCDEFGH,那么编码器输出的第一个字节就是00ABCDEF(该序列就是解码器输入的第一个字节)。现在,如果编码器输入的第二个字节是序列IJKLMNOP,那么编码器输出的第二个字节就是(如图 4.300GHIJKL所示)。
因此,如果序列00ABCDEF和00GHIJKL分别是解码器输入的第一个和第二个字节,则图 4.4直观地演示了这两个字节如何转换为解码器输出的第一个字节。注意,输出字节是序列ABCDEFGH,它是来自编码器输入的原始字节。
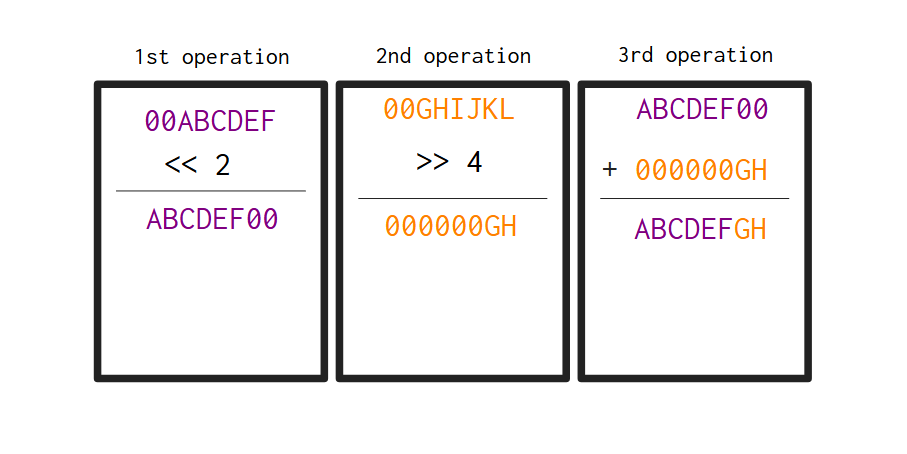
图 4.4:解码器输出中的第一个字节是如何由输入的第一个字节(深紫色)和第二个字节(橙色)生成的
表4.2显示了前面描述的 三个步骤如何转换为 Zig 代码:
表4.2:解码过程中6变换的必要步骤。
| 输出中的字节索引 | 在代码中 |
|---|---|
| 0 | (缓冲区[0] << 2)+(缓冲区[1] >> 4) |
| 1 | (缓冲区[1] << 4)+(缓冲区[2] >> 2) |
| 2 | (缓冲区[2] << 6)+ 缓冲区[3] |
4.5.3编写decode()函数
下面的函数decode()包含整个解码过程。我们首先用 计算输出的大小,_calc_decode_length()然后使用分配器对象为该输出分配足够的内存。
创建了三个临时变量:1) count,用于保存 for 循环每次迭代中的窗口计数;2) iout,用于保存输出中的当前索引;3) buf,用于保存要通过 6 位转换进行转换的 base64 索引的临时缓冲区。
然后,在 for 循环的每次迭代中,我们用当前窗口的字节数填充临时缓冲区。当count命中数字 4 时,我们就有了一个完整的buf待转换索引窗口,然后,我们对临时缓冲区应用 6 位转换。
注意,我们检查了临时缓冲区中的索引 2 和 3 是否为数字 64。如果你还记得4.5.1 节的内容,当_calc_index()函数接收到一个'='字符作为输入时,数字 64 就是这个数字。所以,如果这些索引等于数字 64,decode()函数就知道它可以忽略它们。它们不会被转换,因为正如我之前描述的,尽管该字符'='是序列中有意义字符的结尾,但它没有任何意义。所以当它们出现在序列中时,我们可以放心地忽略它们。
fn decode(self: Base64,
allocator: std.mem.Allocator,
input: []const u8) ![]u8 {
if (input.len == 0) {
return "";
}
const n_output = try _calc_decode_length(input);
var output = try allocator.alloc(u8, n_output);
var count: u8 = 0;
var iout: u64 = 0;
var buf = [4]u8{ 0, 0, 0, 0 };
for (0..input.len) |i| {
buf[count] = self._char_index(input[i]);
count += 1;
if (count == 4) {
output[iout] = (buf[0] << 2) + (buf[1] >> 4);
if (buf[2] != 64) {
output[iout + 1] = (buf[1] << 4) + (buf[2] >> 2);
}
if (buf[3] != 64) {
output[iout + 2] = (buf[2] << 6) + buf[3];
}
iout += 3;
count = 0;
}
}
return output;
}
4.6最终结果
现在我们已经实现了 和decode()。我们在 Zig 中实现了一个功能齐全的 base64 编码器/解码器。下面是我们结构体及其实现的和方法encode()的使用示例。Base64``encode()``decode()
var memory_buffer: [1000]u8 = undefined;
var fba = std.heap.FixedBufferAllocator.init(
&memory_buffer
);
const allocator = fba.allocator();
const text = "Testing some more stuff";
const etext = "VGVzdGluZyBzb21lIG1vcmUgc3R1ZmY=";
const base64 = Base64.init();
const encoded_text = try base64.encode(
allocator, text
);
const decoded_text = try base64.decode(
allocator, etext
);
try stdout.print(
"Encoded text: {s}\n", .{encoded_text}
);
try stdout.print(
"Decoded text: {s}\n", .{decoded_text}
);
Encoded text: VGVzdGluZyBzb21lIG1vcmUgc3R1ZmY=
Decoded text: Testing some more stuff
您还可以通过访问本书的官方存储库3来立即查看完整的源代码。更准确地说,是在ZigExamples文件夹4内。