尽管整数的数量在数学上是无限的，但实际上，计算机内存中的数字类型占用固定数量的位数。正如我们在本章中所暗示的那样，使用固定位数意味着程序可能无法表示它们想要存储的值。例如，对加法的讨论表明，将两个合法值相加可以产生无法表示的结果。缺乏存储空间来表示其结果的计算已溢出。

4.5.1. 里程表仪表盘(Odometer Analogy)

为了描述溢出的特征，考虑一个非计算领域的例子：汽车的里程表。里程表计算汽车行驶的里程数，无论是数字式还是模拟式，它只能显示这么多（以 10 为基数）数字。如果汽车行驶的里程数超过了里程表所能表示的里程数，里程表就会“翻转”回零，因为无法表达真实值。例如，对于标准的六位里程表，它表示的最大值是 999999。再行驶一英里应该显示 1000000，但是像溢出加法示例 一样，1 从六位可用数字中执行，只留下000000。

为简单起见，让我们继续分析仅限一位小数的里程表。也就是说，里程表代表范围 [0, 9]，因此每行驶 10 英里后里程表就会重置为零。直观地说明里程表的范围，它可能看起来像图 1。 A circle with the values 0 to 9 arranged around it. 图 1. 一位数里程表潜在值的直观描述

由于一位数的里程表在达到 10 时会翻转，因此绘制圆形会强调圆顶部（并且仅在顶部）的不连续性。具体来说，通过将 1 与除 9 之外的任何值相加，结果将达到预期值。另一方面，添加一到九会跳转到一个不自然跟随它的值（零）。更一般地说，当执行任何跨越九和零之间不连续性的算术时，计算将会溢出。例如，考虑添加 8 + 4，如 图 2 所示。

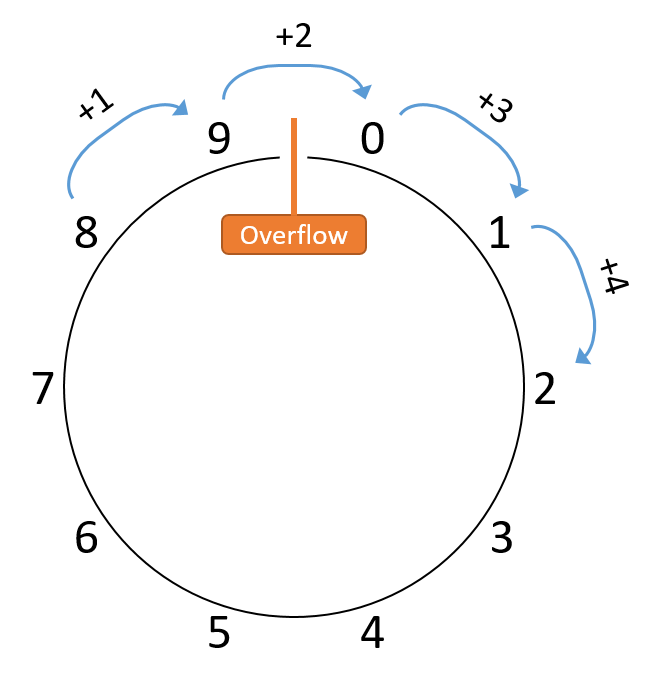A circle with the values 0 to 9 arranged around it. The gap between 0 and 9 is labeled as the location where overflow can occur. Arrows show that adding 4 to 8 causes the arithmetic to jump across the marked overflow location. 图 2. 8 + 4 相加的结果，仅保留一位小数。跨越 0 和 9 之间的不连续性表示发生了溢出。

在这里，总和得到 2，而不是预期的 12。请注意，与 8 相加的许多其他值（例如，8 + 14）也将得到 2，唯一的区别是计算将需要绕圈进行额外的行程。因此，无论汽车行驶2英里、12英里还是152英里，最终里程表的读数都是2。

任何行为类似于里程表的设备都执行模运算。在这种情况下，所有算术都是以模 10 为模数的，因为一位十进制数字仅代表 10 个值。因此，给定任意行驶里程数，我们可以通过将距离除以 10 并将余数作为结果来计算里程表的读数。如果里程表有两位小数而不是一位，则模数将更改为 100，因为它可以表示更大的值范围：[0, 99]。同样，时钟以小时模数 12 执行模算术。

4.5.2. 二进制整数溢出

看过熟悉的溢出形式后，让我们转向二进制数字编码。回想一下，N 位存储代表 2N 个唯一的位序列，并且这些序列可以用不同的方式解释（如 无符号 或 有符号）。在一种解释下产生正确结果的某些操作可能会根据另一种解释而出现溢出，因此硬件需要针对每种解释以不同的方式识别溢出。

例如，假设机器使用四位序列来计算 0b0010 (2) - 0b0101 (5)。通过减法过程 运行此运算会生成二进制结果 0b1101。将此结果解释为有符号值会产生 -3 (-8 + 4 + 1)，即 2 - 5 的预期结果（无溢出）。或者，将其解释为 无符号 值会产生 13 (8 + 4 + 1)，这是不正确的并且清楚地表明溢出。进一步审视这个例子，它本能地有一定道理——结果应该是负数，有符号的解释允许负数，而无符号的则不允许。

无符号溢出

无符号 数字的行为与十进制里程计示例类似，因为两者都只表示非负值。 N 位表示 [0, 2N- 1] 范围内的无符号值，使所有算术都以 2N 为模数。 图 3 展示了四位序列的无符号解释在模块化空间中的排列。

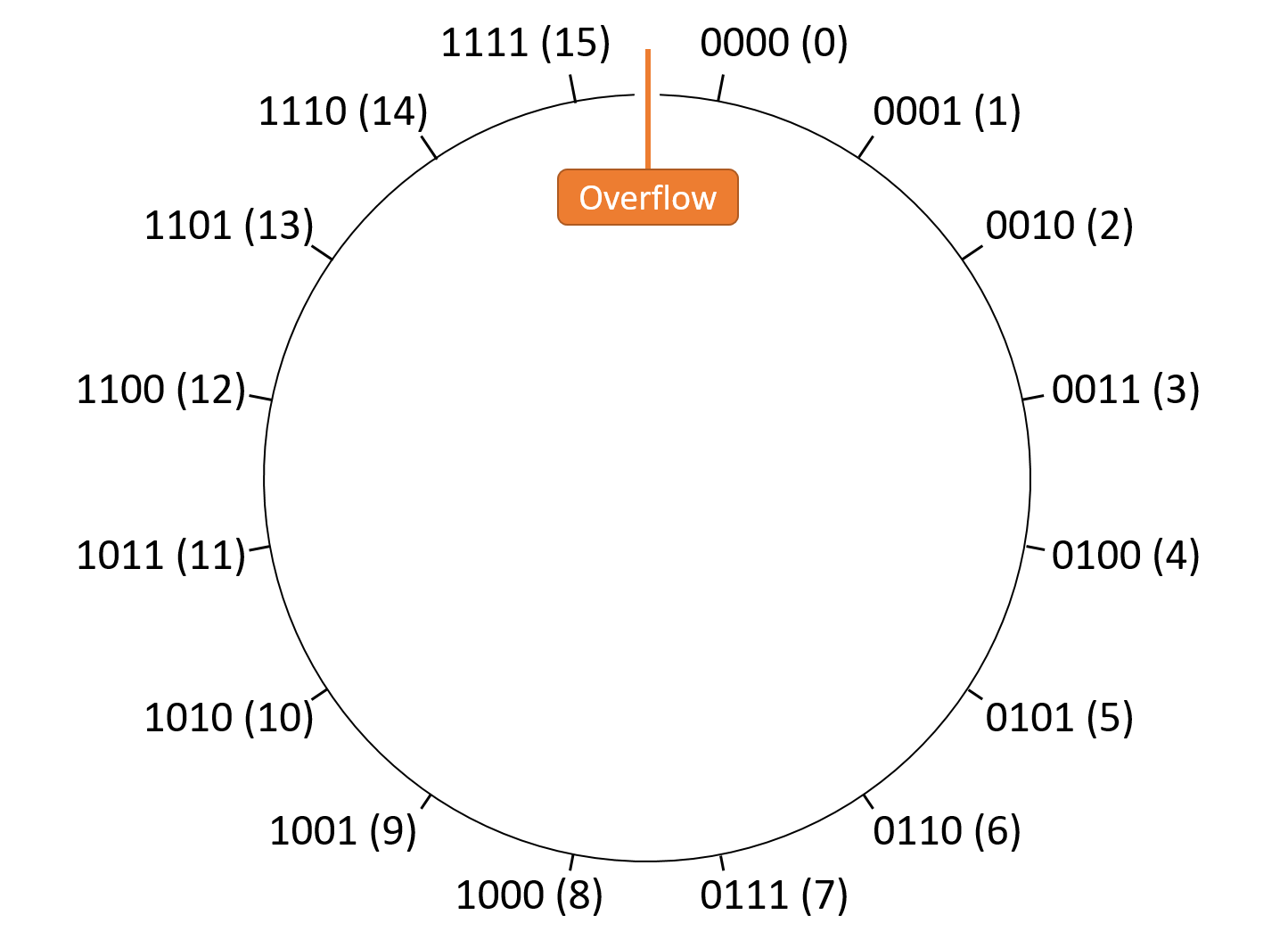The numbers 0 to 15 are arranged in a circle. The gap between 15 and 0 (at the top of the circle) is labeled as the location where overflow can occur. 图 3. 四位无符号值在模空间中的排列。所有算术都是关于 24 (16) 的模数。

鉴于无符号解释不能容纳负值，不连续性再次位于最大值和零之间。因此，任何跨越 2N-1和 0 之间除法的操作都会导致无符号溢出。更简单地说，如果执行加法（这应该使结果 更大）产生较小的结果，则加法会导致无符号溢出。对称地，如果执行减法（这应该使结果 更小）产生更大的结果，则减法会导致无符号溢出。

作为检测加法和减法无符号溢出的快捷方式，请回忆一下这些运算的 carry out 和 carry in位。 carry out 是计算结果中最高有效位的进位。设置后，carry in 通过将 1 进位到算术运算的最低有效位来增加结果的值。作为求反过程的一部分，carry in 仅设置为 1 以进行减法。

无符号算术的快捷方式是：carry out必须与carry in匹配，否则运算会导致溢出。直观上，这个快捷方式之所以有效，是因为：

  • 对于加法 (carry in = 0)，结果应大于（或等于）第一个操作数。但是，如果总和需要额外的存储位(carry out = 1)，则从总和中截断该额外位会产生较小的结果（溢出）。例如，在无符号四位数字空间中，添加 0b1100 (12) + 0b1101 (13) 需要 五个 bit位来存储结果 0b 11001 (25)。当截断为只有四位时，结果表示 0b1001 (9)，它小于操作数（因此，溢出）。
  • 对于减法（carry in = 1），结果应小于（或等于）第一个操作数。由于减法是作为加法和求反的组合执行的，因此减法问题应该产生较小的结果。加法最终得到较小值的唯一方法是截断其总和（carry out = 1）。如果不需要截断（carry out = 0），减法会产生更大的结果（溢出）。

让我们看一下四位减法的两个例子：一个溢出，一个不溢出。首先，考虑 0b0111 (7) - 0b1001 (9)。减法过程将此计算视为：

Problem SetupConverted to AdditionWorked Example
&nbsp&nbsp&nbsp0111
- 1001		&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp1 (carry in)
&nbsp&nbsp&nbsp0111
+ 0110 (bits flipped)		&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp1 (carry in)
&nbsp&nbsp&nbsp0111
+ 0110 (bits flipped)

Result: 1110
Carry out: 0

计算 没有 从 d3 中进位(carry out)，因此不会发生截断，并且 (1) 中的进位(carry in)无法匹配进位 (0)。结果 0b1110 (14) 比任一操作数都大，因此对于 7 - 9 显然是不正确的（溢出）。

接下来，考虑 0b0111 (7) - 0b0101 (5)。减法过程将此计算视为：

Problem SetupConverted to AdditionWorked Example
&nbsp&nbsp&nbsp0111
- 0101		&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp1 (carry in)
&nbsp&nbsp&nbsp0111
+ 1010 (bits flipped)		&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp1 (carry in)
&nbsp&nbsp&nbsp0111
+ 1010 (bits flipped)

Result: 0010
Carry out: 1

计算对 d4 执行一位，导致 (1) 中的进位与 (1) 中的进位匹配。截断结果 0b0010 (2) 正确表示减法运算的预期结果（无溢出）。

有符号溢出

溢出背后的相同直觉也适用于有符号二进制解释：模数空间中存在不连续性。然而，由于有符号解释允许负数，因此在 0 附近不会出现不连续性。回想一下，二进制补码 干净利落地从 -1 (0b1111…​111)“翻转”到 0 (0b0000…​000)。因此，不连续性存在于数字空间的另一端，即最大正值和最小负值相遇的地方。

图 4 显示了四位序列的带符号解释在模块化空间中的排列。请注意，一半值是负值，另一半是非负值，并且不连续性位于它们之间的最小/最大分界处。

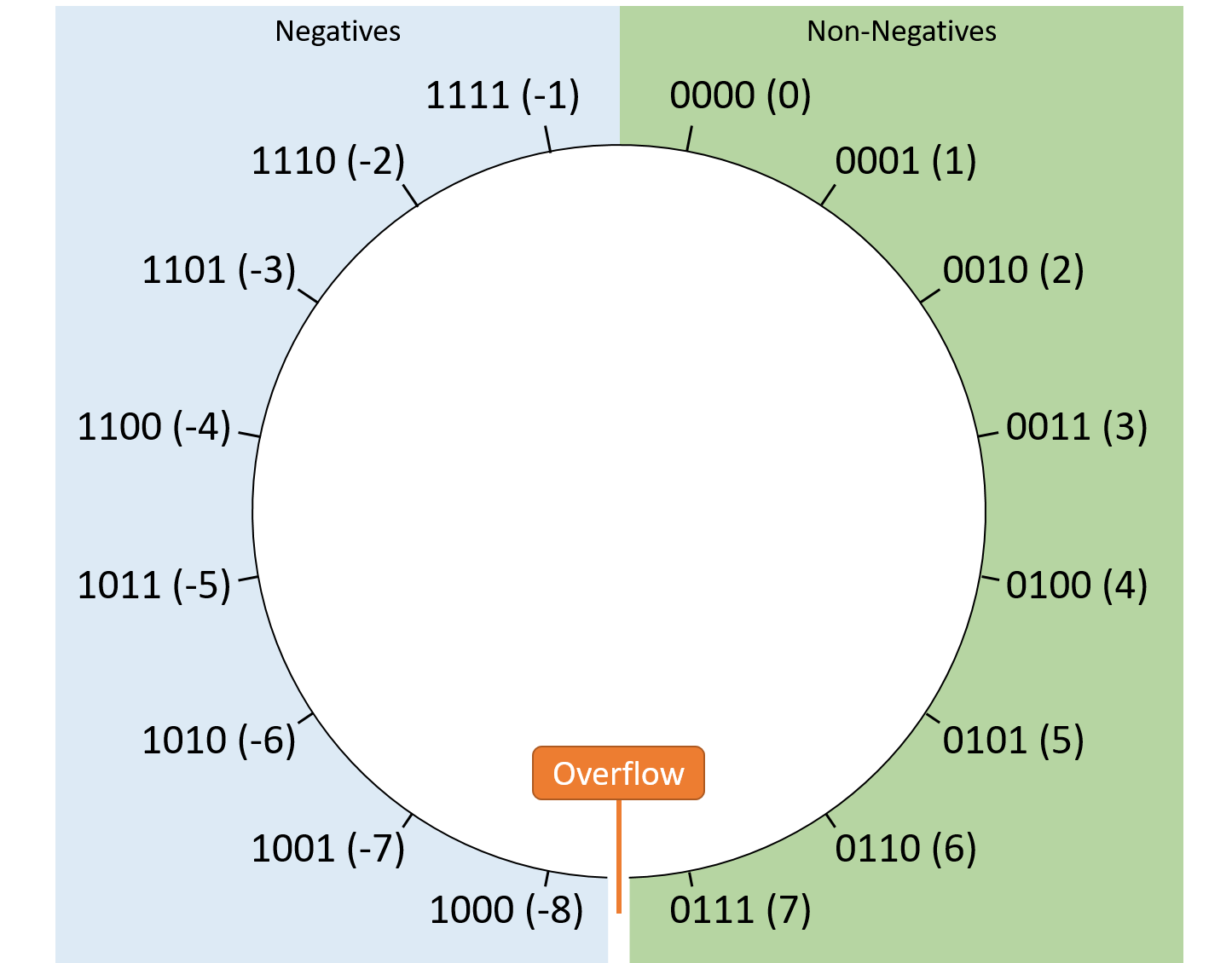The numbers 0 to 7 are arranged on the right half of a circle, and the numbers -1 to -8 are arranged on the left half. The gap between 7 and -8 (at the bottom of the circle) is labeled as the location where overflow can occur. 图 4. 四位有符号值在模空间中的排列。由于带符号的解释允许负值，因此不连续性不再位于零。

执行有符号算术时，生成接近零的结果始终是安全的。也就是说，任何减少结果绝对值的操作都不会溢出，因为溢出不连续性存在于可表示值的幅度最大的地方。

因此，系统通过将操作数的最高有效位与结果的最高有效位进行比较来检测带符号加法和减法中的溢出。对于减法，首先根据加法重新排列算术（例如，将 5 - 2 重写为 5 + -2）。

  • 如果加法的操作数具有 不同 高位值（即，一个操作数为负，另一个为正），则不会有符号溢出，因为结果的绝对值必须小于（或等于）任一操作数。结果是朝 _零方向移动。
  • 如果加法的操作数具有相同的高位值（即均为正或均为负），则正确的结果也必须具有相同的高位位值。因此，当将两个具有相同符号的操作数相加时，如果结果的符号与操作数的符号不同，则会发生有符号溢出。

考虑以下四位有符号二进运算示例：

  • 5 - 4 相当于 5 + -4。第一个操作数 (5) 为正，而第二个操作数 (-4) 为负，因此结果必须向零移动，其中 不会溢出。
  • 4 + 2（均为正数）产生 6（也是正数），因此 不会发生溢出。
  • -5 - 1 相当于 -5 + -1（均为负数）并产生 -6（也是负数），因此 不会发生溢出。
  • 4 + 5（均为正数）产生 -7（负数）。由于操作数具有相同的符号，但与结果的符号不匹配，因此此操作 溢出。
  • -3 - 8 相当于 -3 + -8（均为负数）并产生 5（正数）。由于操作数具有相同的符号，但与结果的符号不匹配，因此此操作 溢出。

4.5.3. 溢出总结

一般来说，当算术运算在其结果可以表示的最小值和最大值之间移动时，就会发生整数溢出。如果您对有符号溢出和无符号溢出的规则有疑问，请考虑 N 位序列的最小值和最大值：

  • 最小 unsigned 值为 0（因为无符号编码不能表示负数），最大无符号值为 2N-1（因为一位序列保留为零）。因此，不连续性在 2N-1 和 0 之间。
  • 最小 signed 值为 -2N-1（因为一半序列保留为负值），最大值为2N-1-1（因为在另一半中，一个值保留为零）。因此，不连续性介于 2N-1-1 和 -2N-1 之间。

4.5.4. 溢出后果

虽然您可能不会经常遇到整数溢出，但溢出有可能以显着（并且可能具有破坏性）的方式破坏程序。

例如，2014 年，PSY 流行的江南 Style 音乐视频可能会溢出 YouTube 用于跟踪视频点击率的 32 位计数器。因此，YouTube 转而使用 64 位计数器。

另一个相对无害的例子出现在 1980 年的街机游戏 吃豆人 中。游戏开发者使用无符号的八位值来跟踪玩家在游戏关卡中的进度。因此，如果专家玩家的级别超过 255 级（八位无符号整数的最大值），那么一半的棋盘最终会出现严重故障，如图5所示。

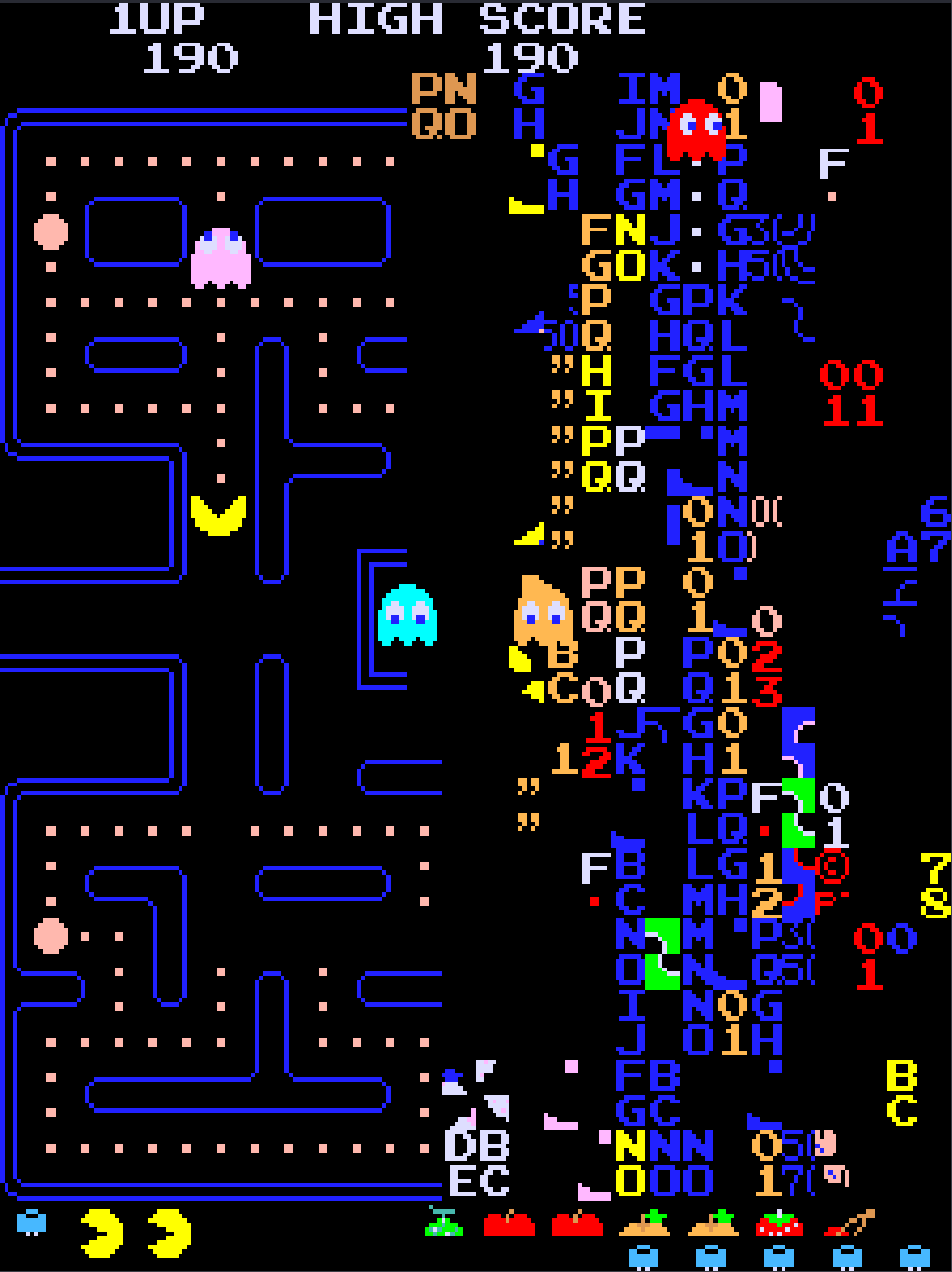The right half of the game board is completely corrupted with nonsense. 图 5. Pac-Man 游戏板在达到 256 级时“吓坏了”

一个更悲惨的溢出例子出现在 20 世纪 80 年代中期的 Therac-25 放射治疗机的历史中。 Therac-25 存在多个设计问题，其中一个问题是增加真值标志变量而不是将其设置为常量。经过足够的使用后，标志溢出，导致其错误地翻转到零（假）并绕过安全机制。 Therac-25 最终对 6 名患者造成严重伤害（在某些情况下甚至导致死亡）。